可见光OCT是近年来新兴的一种高分辨率OCT成像技术,其相比于传统的近红外OCT技术,分辨率可以提升5-10倍,而且具有血氧饱和度测量等光谱学分析能力,具有广泛的应用前景。但是,相比于近红外波段,OCT成像在可见光波段的色散失配问题更加严重,存在着较为严重的高阶色散,并且存在着空间相关色散(SDD)的问题,这都将会导致系统点扩散函数(PSF)的展宽与变形,进而导致分辨率的下降。因为,开发一种新的色散补偿技术以高效、准确地补偿可见光OCT成像系统中的高阶色散、空间相关色散等问题,具有重要应用价值与意义。针对上述挑战,山东大学宋维业教授课题组提出了一种新的色散补偿算法,该算法通过对系统中引起色散的光学元件相位的计算与建模,对系统的色散不平衡相位进行精确补偿,可以实现高阶色散的有效补偿,并且可以通过计算扫描过程中的色散相位变化,实现空间相关色散的补偿。该成果以“Phase Modeling of Optical Components for Dispersion Compensation in Visible Light OCT”为题发表在《IEEE Photonics Technology Letters》期刊上。
研究背景
光学相干断层扫描(OCT)是一种非侵入式成像技术,能够获取样本的高分辨率三维图像,广泛应用于视网膜成像、生物组织分析及工业无损检测等领域。可见光OCT(vis-OCT)作为OCT的重要分支,利用可见光波段(通常为500-650 nm)的短波长和宽光谱特性,可实现亚微米级分辨率的成像,但这也带来了严重的色散失配问题。色散失配会导致点扩散函数展宽和不对称畸变,从而降低图像分辨率和信噪比(SNR)。现有色散补偿方法主要分为硬件补偿和数字补偿两类:硬件方法通过添加匹配光学组件(如玻璃片、棱镜对、水槽等)进行补偿,但需精密光学对准,系统复杂;数字方法包括校准型(如DCSPM、SAMMR)和样本型(如分数傅里叶变换)等,前者需采集镜面反射信号进行校准,后者易受噪声和样本结构影响。其中,泰勒级数迭代拟合(TSIF)方法无需镜面反射信号或样品信号的校准,其通过迭代优化二阶和三阶色散系数实现补偿,在近红外OCT成像中得到广泛应用,但难以处理vis-OCT中的高阶色散问题。此外,空间依赖性色散(SDD)因扫描透镜中光束路径长度变化而产生,进一步加剧了成像不均一性。Kho和Srinivasan曾提出子带相关算法进行SDD估计,但该方法计算复杂。因此,开发一种简单、高效且能补偿高阶色散和SDD的方法成为提升vis-OCT成像质量的重要挑战。
研究方法
本研究提出的PMOC方法基于光学组件的相位建模,其核心思想是通过计算光路中各组件产生的色散相位,对其进行数字补偿。算法流程如图1所示。方法流程包括传统OCT图像重建、相位提取及补偿相位计算等步骤。首先,对干涉信号进行直流扣除和线性k插值预处理,然后通过希尔伯特变换生成复解析干涉信号。色散补偿相位由各光学组件的相位贡献叠加而成,其中单个组件的相位ϕ(z)取决于光束穿过组件的厚度z和元件材料的折射率。折射率由Sellmeier方程计算得到,该方程可以基于经验系数计算得到不同波长下的折射率。PMOC方法通过迭代优化组件厚度参数z1,z2,…,zm,以最大化评价指标函数M(定义为OCT图像中超过预设阈值的像素数倒数),实现最优补偿效果。与TSIF方法仅优化低阶(二阶和三阶)色散系数不同,PMOC利用Sellmeier方程计算系统中光学组件所引起的色散相位,包含了各阶色散的相位信息,从而可以实现高阶色散的补偿。此外,针对SDD问题,PMOC通过计算扫描透镜中不同位置的光束路径长度变化,推导相应相位变化进行补偿,计算过程直观简单,无需复杂计算。
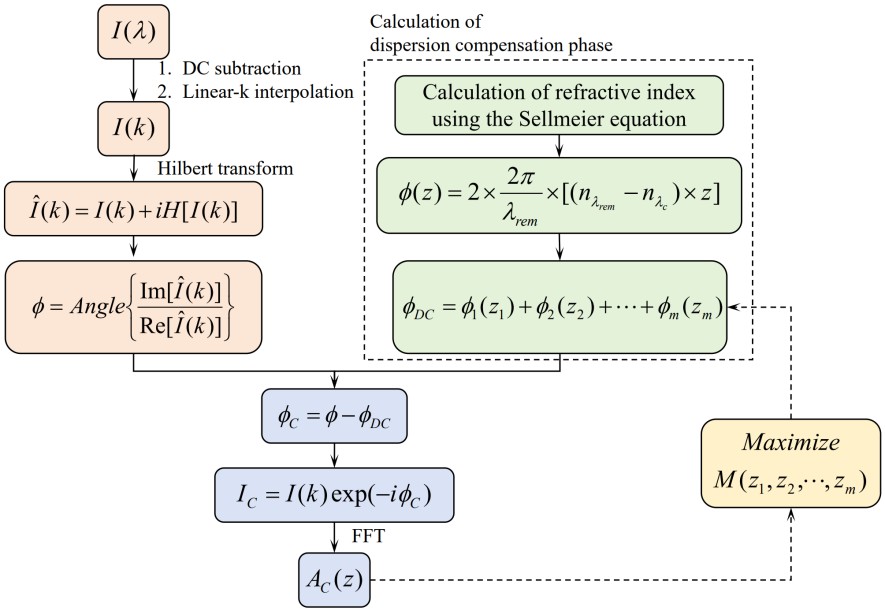
图1. PMOC方法在OCT系统中进行色散补偿的流程图
实验结果
首先,搭建了一套可见光波段的迈克尔逊干涉仪系统,采集干涉信号进行色散补偿算法的验证。通过插入不同厚度的BK7和N-LASF43平面窗口引入色散失配。结果显示,在无色散失配情况下,PSF的半高全宽(FWHM)为1.97μm;随着色散失配增加,高阶色散的影响变得越来越明显,TSIF方法处理得到的PSF出现分辨率下降、不对称性和旁瓣严重等问题,而PMOC方法在所有情况下均保持与无色散情况相似的PSF。例如,在最大色散失配条件(FW1+FW2)下,TSIF导致FWHM展宽0.54 μm,而PMOC仅展宽0.05 μm,分辨率提升达10倍。PMOC方法优化得到的光学元件厚度参数与实际值高度吻合(如表1所示),验证了PMOC算法的色散补偿的有效性和准确性。此外,PMOC在深度范围内的轴向分辨率和灵敏度滚降均优于TSIF。PMOC方法计算得到的色散补偿相位误差最大不超过2弧度,远低于TSIF的20弧度以上。
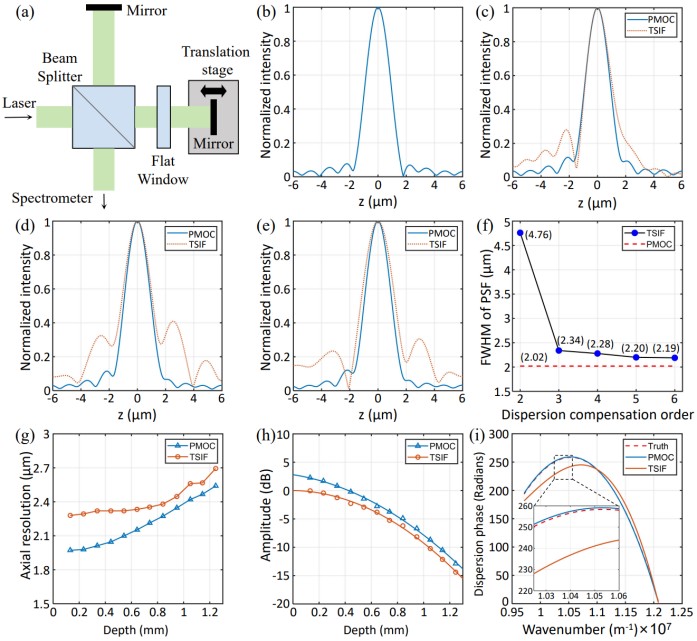
图2. 使用PMOC和TSIF方法对干涉信号进行色散补偿效果对比。(a) 迈克尔逊干涉仪系统示意图; (b) 无色散失配情况下获得的PSF; (c)-(e) 在干涉臂中放置不同平面窗口时的PSF对比; (f) TSIF方法不同补偿阶数的PSF半高全宽比较; (g) 整个成像深度范围内的轴向分辨率对比; (h) 整个成像深度范围内的灵敏度滚降特性对比; (i) PMOC和TSIF提取的色散相位与真实相位对比。
表1. 平面窗口参数以及PMOC和TSIF方法获得的PSF半高全宽

然后,搭建了可见光OCT系统对PMOC在OCT成像中的色散补偿效果进行了验证。在成像时,样品臂中使用一个双胶合透镜作为扫描物镜,参考臂中不放置任何光学元件进行色散补偿,分别对镜面和胶带进行了扫描成像,结果如图3所示。在镜面B-scan图像中,PMOC得到的镜面图像的FWHM为2.02 μm(十分接近无色散失配时的PSF分辨率),第一旁瓣幅值为99.4 dB,SNR为62.3 dB;而由TSIF得到的分别为2.84 μm、107.3 dB和59.3 dB。在胶带图像中,PMOC得到的图像在整个深度范围内均表现出更清晰的层状结构和更低的噪声,进一步证明了PMOC的色散补偿效果。
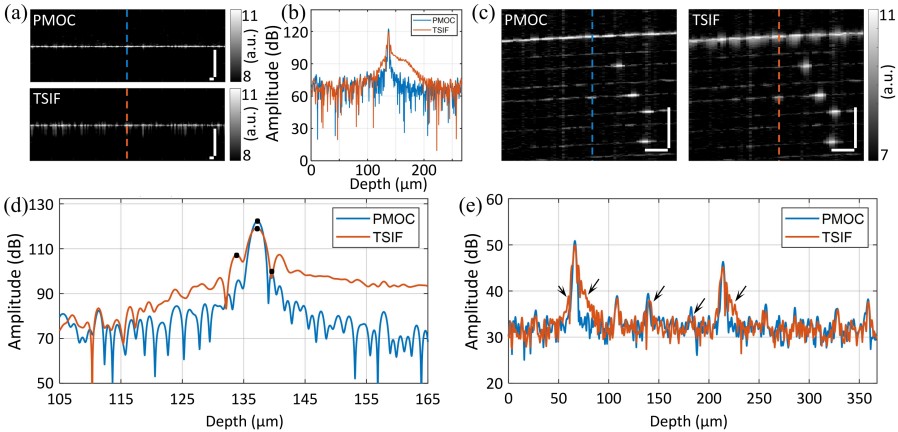
图3. OCT图像色散补偿性能比较。(a) PMOC和TSIF获得的镜面B-scan图像; (b) 对应(a)中虚线位置的A-line信号; (c) 使用PMOC和TSIF获得的胶带B-scan图像; (d) (b)中A-line信号的放大视图; (e) 对应(c)中虚线位置的A-line信号。
最后,在SDD补偿验证中,在样品臂中使用一个非对称双凸透镜作为扫描透镜,此时在参考臂中放置一个相同的透镜进行物理色散补偿。在PMOC算法中通过计算不同扫描位置的光束路径长度变化进行补偿,TSIF方法通过优化二阶和三阶色散系数进行色散补偿,实验结果如图4所示。原始镜面图像在图像的扫描视场边缘区域出现明显的分辨率降低,图像变得模糊。使用TSIF补偿后,视场边缘区域的分辨率得到提升但中心区域的图像分辨率降低,无法同时实现整个扫描视场范围内的高精度色散补偿,而PMOC处理后的图像在整个视场内分辨率均保持在最佳或接近最佳的状态,边缘区域的镜面视觉厚度由原始图像中的中心区域图像厚度的2倍降至和中心区域接近的水平。上述结果证明了PMOC在SDD补偿中的有效性。
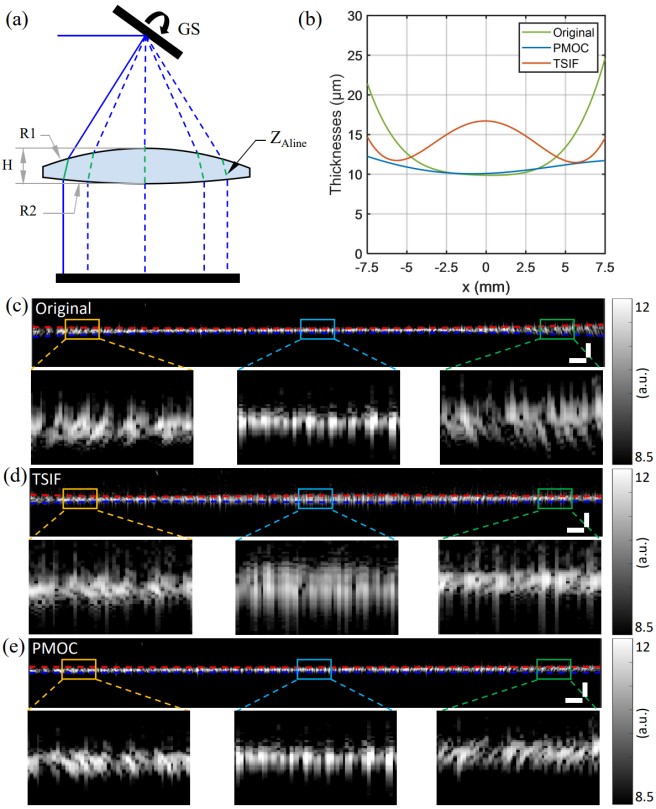
图4. SDD补偿结果分析与对比。 (a) OCT扫描路径示意图; (b) 有无SDD补偿的镜面图像厚度比较; (c) 原始镜面图像; (d) 使用TSIF进行色散补偿得到的图像; (e) 使用PMOC进行SDD补偿得到的图像。
实验结论
本论文提出了一种基于光学元件色散相位建模的新型色散补偿方法(PMOC),能够有效解决vis-OCT中的高阶色散和空间相关色散问题。实验结果表明,PMOC进行色散补偿得到的图像在分辨率、SNR等方面均优于广泛使用的TSIF方法,且无需复杂校准或额外测量。该方法计算简单、补偿精度高,使用PMOC方法进行色散补偿实现了与无色散条件相当的图像质量。
该研究得到了国家自然科学基金、山东省自然科学基金等项目的支持。